Volume 3: 1771 Edition of the Encyclopedia Britannica!

Neper's Rods, or Bones

Neper's Rods, or Bones, an instrument invented by J. (John) Neper (Napier), baron of Merchiston, in Scotland, whereby the multiplication and division of large numbers are much facilitated.

As to the construction of Neper's Rods: suppose the common table of multiplication to be made upon a plate of metal, ivory, or paste-board, and then conceive the several columns (standing downwards from the digits on the head) to be cut asunder; and these are what we call Neper's rods for multiplication. But then there must be a good number of each; for as many times as any figure is in the multiplicand, so many rods of that species (i.e. with that figure on the top of it) must we have; though six rods of each species will be sufficient for any example in common affairs: there must also be as many rods of 0's (zeros).

But before we explain the way of using these rods, there is another thing to be known, viz. that the figures on every rod are written in an order different from that in the table. Thus, the little square space or division in which the several products of every column are written, is divided into two parts by a line across from the upper angle on the right to the lower on the left; and if the product is a digit, it is set in the lower division; if it has two places, the first is set in the lower, and the second in the upper division; but the spaces on the top are not divided; also there is a rod of digits, not divided, which is called the index rod, and of this we need but one single rod. See the figure of all the different rods, and the index, separate from one another, in Plate CXXXIV, fig. 1.

Multiplication by Neper's Rods. First lay down the index rod; then on the right of it set a rod whose top is the figire in the highest place of the multiplicand; next to this again, set the rod, whose top is the next figure of the multiplicand; and so on in order, to the first figure. Then is your multiplicand tabulated for all the nine digits; for in the same line of squares standing against every figure of the index rod, you have the product of that figure, and therefore you have no more to do but to transfer the products and sum them. But in taking out these products from the rods, the order in which the figures stand obliges you to a very easy and small addition; thus, begin to take out the figure in the lower part, or unit's place, of the square of the first rod on the right; add the figure in the upper part of this rod to that in the lower part of the next, and so on, which may be done as fast as you can look on them. To make this practice as clear as possible, take the following example.

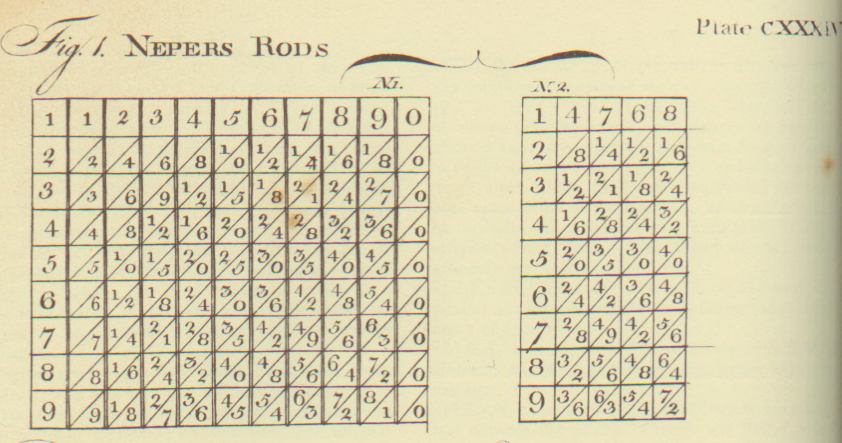
Example: To multiply 4768 by 385. Having set the rods together for the number 4768 (ibid No. 2.)

against 5 in the index, I find this number by adding according to the rule:  23840
against 8, this number                                                      38144
against 3, this number                                                     14304
                                                                         ---------
                       Total Product                                       1835680

To make the use of the rods yet more regular and easy, they are kept in a flat square box, whose breadth is that of ten rods, and the length that of one rod, as thick as to hold six (or as many as you please) the capacity of the box being divided into ten cells for the different species of rods. When the rods are put up in the box (each species in its own cell distinguished by the first figure of the rod set before it on the face of the box near the top) as much of every rod stands without the box as shews the first figure of that rod; also upon one of the flat sides without and near the edge, upon the left hand, the index rod is fixed; and along the foot there is a small ledge, so that the rods when applied are laid upon this side, and supported by the ledge, which makes the practice very easy; but in case the multiplicand should have more than nine places, that upper face of the box may be made broader. Some make the rods with four different faces, and figures on each for different purposes.

Division by Neper's Rods. First tabulate your divisor; then you have it multiplied by all the digits, out of which you may chuse such convenient divisors as will be next less to the figures in the dividend, and write the index answering in the quotient, and so continually till the work is done. Thus 2179788, divided by 6123, gives the quotient 356.

Having tabulated the divisor 6123, you see that 6123 cannot be had in 2179; therefore take five places, and on the rods find a number that is equal or next less to 21797, which is 18369; that is, 3 times the divisor; wherefore set 3 in the quotient, and subtract 18369 from the figures above, and there will remain 3428; to which add 8, the next figure of the dividend, and seek again on the rods for it, or the next less, which you will find to be five times; therefore set 5 in the quotient, and subtract 30615 from 34288, and there will remain 3673; to which add 8, the last figure in the dividend, and finding it to be just 6 times the divisor, set six in the quotient.

              6123) 2179788 (356
                    18369
                   ------
                     34288
                     30615
                    ------
                      36738
                      36738
                     ------
                      00000

Side Note: In the year 1623, Wilhelm Schickard, Professor at the University of Tuebingen, designed and built a mechanical calculator based on Neper's rods that did, in fact, add-subtract-multiply-divide.

Click here for the index to Volume 1: A-B

Click here for the index to Volume 2: C-L

Click here for the index to Volume 3: M-Z

Click here for the index to the 1771 Encyclopedia

---

This Encyclopedia project is brought to you by the American Conservatory of Music and the Orthodox Church of Belize. This Web Site and all content therein to the extent permissible by law is Copyright © 2006 by the American Conservatory of Music. All Rights Reserved. Permission to copy from this web site is freely granted as long as credit is given to the American Conservatory of Music. However, mirroring of this web site is not permitted.